自动驾驶汽车路径规划算法浅析
自动驾驶汽车路径规划算法浅析自动驾驶汽车的路径规划算法最早源于机器人的路径规划研究,但是就工况而言却比机器人的路径规划复杂得多,自动驾驶车辆需要考虑车速、道路的附着情况、车辆最小转
自动驾驶汽车的路径规划算法最早源于机器人的路径规划研究,但是就工况而言却比机器人的路径规划复杂得多,自动驾驶车辆需要考虑车速、道路的附着情况、车辆最小转弯半径、外界天气环境等因素。
本文将为大家介绍四种常用的路径规划算法,分别是搜索算法、随机采样、曲线插值和人工势场法。
1.搜索算法
搜索算法主要包括遍历式和启发式两种,其中Dijkstra算法属于传统的遍历式,A*算法属于启发式,在A*算法的基础上,还衍生出了D*Lite算法、Weighted A*算法等其他类型。Dijkstra算法最早由荷兰计算机学家狄克斯特拉于1959年提出,算法核心是计算从一个起始点到终点的最短路径,其算法特点是以起始点开始向周围层层扩展,直到扩展到终点为止,再从中找到最短路径,算法搜索方式如图(1-1)所示。A*算法在Dijkstra算法上结合了最佳优先算法,在空间的每个节点定义了一个启发函数(估价函数),启发函数为当前节点到目标节点的估计值,从而减少搜索节点的数量从而提高效率。A*算法中的启发函数
包括两部分,表示从初始点到任意节点n的代价,表示节点n到目标点的启发式评估代价,在对象从初始点开始向目标点移动时,不断计算的值,从而选择代价最小的节点。一般来说遍历式算法可以取得全局最优解,但是计算量大,实时性不好;启发式算法结合了遍历式算法以及最佳优先算法的优点,具有计算小、收敛快的特点。图(1-2)是最佳优先算法示意图,可以看出该算法有一定的选择性,但是面对图中的u型障碍物会出现计算效率低的情况。而A*算法完美的结合了Dijkstra算法和最佳优先算法,不仅有一定的选择性,并且计算量相对也是最少的,更快得找到了最短路径。

图1-1 Dijkstra算法示意图
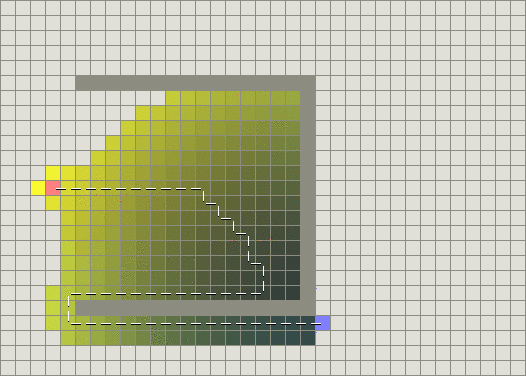
图1-2 最佳优先算法示意图
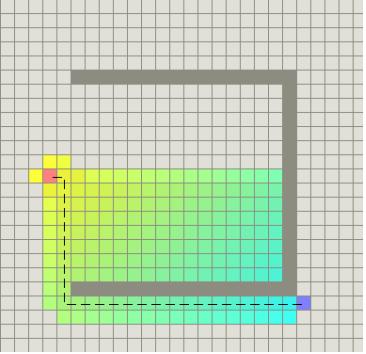
图1-3 A*算法示意图
2.随机采样
随机采样主要包括蚁群算法以及RRT(快速扩展随机树)算法。蚁群算法是由Dorigo M等人于1991年首先提出,并首先使用在解决TSP(旅行商问题)上。其算法基本原理如下:1.蚂蚁在路径上释放信息素。2.碰到还没走过的路口,随机选一条走,同时释放与路径长度有关的信息素。3.信息素浓度与路径长度成反比。后来蚂蚁再次碰到该路口时,就选择信息浓度较高的路径。4.最优路径上的信息素浓度越来越大。5.信息素浓度最大的路径为最优路径。其在小规模TSP中性能尚可,再大规模TSP问题中性能下降,容易停滞。实际道路环境是比较复杂的,不光有道路、障碍物等的限制,也有其自身动力学的约束,所以该算法更适合做全局路径规划,不太适合局部路径规划。
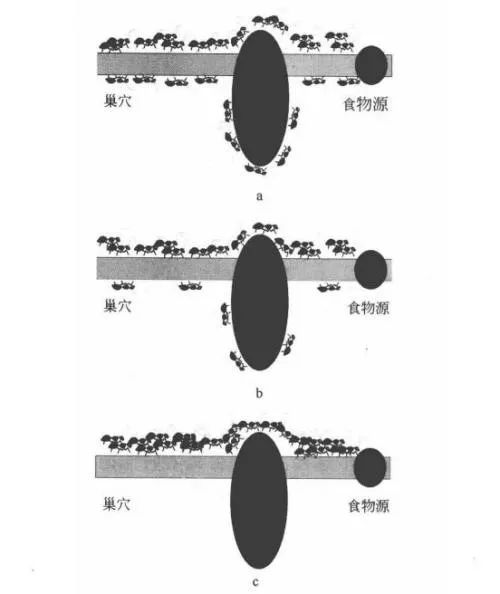
图2-1 蚁群算法示意图
3.曲线插值
曲线插值的方法是按照车辆在某些特定条件(安全、快速、高效)下,进行路线的曲线拟合,常见的有贝塞尔曲线、多项式曲线、B样条曲线等。一般就多项式算法而言,主要考虑以下几个几何约束,从而确定曲线的参数。几何约束:1.起始点的位置与姿态。2.最小转弯半径。3.障碍物约束。4.目标点的位置与姿态。根据考虑的几何约束不同,多项式算法的阶数从三阶到六阶甚至更高阶,阶数越高的算法复杂度越高,收敛速度越慢。四次多项式的形式如式(3-1)所示,参数由几何约束条件确定。基于参数化曲线来描述轨迹,这种类型的算法比较直观,也可以更加准确的描述车辆所需满足的道路条件,规划出的轨迹也十分平坦、曲率变化连续并可进行约束。缺点是计算量较大,实时性不太好,并且其评价函数也比较难以找到最优的,未来的研究方向主要集中于简化算法以及更加完善的评价函数。目前,曲线拟合算法是采用比较广泛的规划方法。
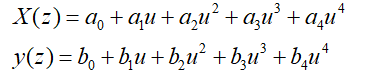
(3-1)
4.人工势场法
人工势场法(Artificial PotentialField,APF)是由Khatib于1986年提出的。该算法是假设目标点会对自动驾驶车辆产生引力,障碍物对自动驾驶车辆产生斥力,从而使自动驾驶车辆沿“势峰”间的“势谷”前进。这种算法的优点就是结构简单,有利于底层控制的实时性,可大大减少计算量和计算时间,并且生成相对光滑的路径,利于保持自动驾驶车辆的稳定性。算法的缺点是有可能陷入局部最优解,难以对规划出的路径进行车辆动力学约束,复杂环境下的势场搭建也比较棘手。势场的基本步骤如下:首先搭建势场,包括障碍物势场以及目标点势场,然后通过求势场负梯度,可以得到车辆在势场中所受的障碍物斥力以及目标点引力。将所受的所有障碍物斥力与目标点引力叠加,就可以得到车辆在势场中任意位置的受力情况,最后根据合力情况不断迭代更新位置,就可以得到从起始点到终点的完整路径。
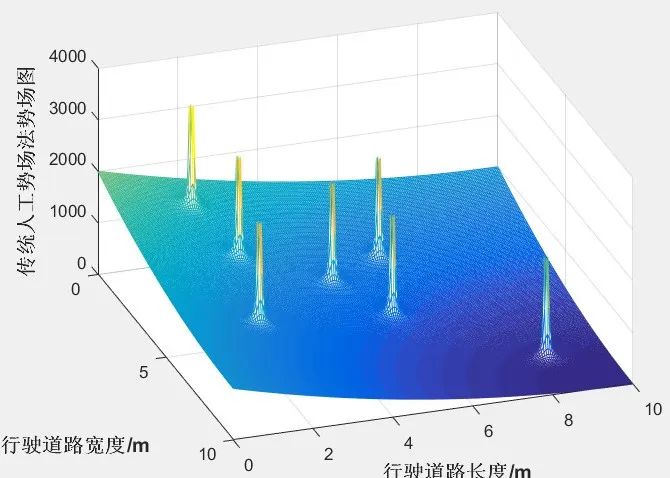
图4-1 基于人工势场法搭建的势能场
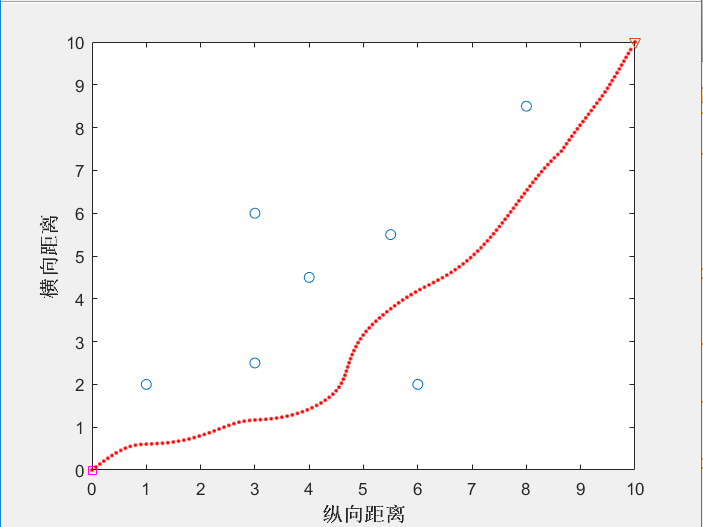
图4-2 基于人工势场法规划的路径点
最后以下表对本文介绍的四种算法的优缺点、计算效率进行一个简要的对比总结。不难发现,其中人工势场法的计算速度最快,实时性也最好,但是存在局部最优解、复杂势场难以搭建的情况,这也是未来该算法的研究热点、难点;其中,曲线插值是目前较常见的一种算法,虽然该算法的计算效率不高,但是相信在未来车载计算机的计算能力大幅度提升之后,该算法可以被更广泛得使用。

-
智能算法全面升级 2000元档性价比新擂主!2020-03-04
-
3D打印新操作 智能算法助你随心设计专属人像模型2020-03-04
-
3D打印新操作 | 智能算法助你随心设计专属人像模型2020-03-04
-
搭载声加科技SVE三麦克风通话降噪算法 荣耀Flypods3正式发售2020-03-02
-
腾讯优图开发出新算法,能精准识别戴着口罩的人脸2020-02-24
-
科学家研发新型AI算法 首次独立发现抗生素分子2020-02-24
-
仙知激光SLAM导航融合多传感器算法,让移动机器人更稳定、更智能!2020-02-21
-
滴滴研发机器人AI算法:秒级识别口罩佩戴、免费开放2020-02-20
-
一汽轿车资产重组过会 一汽集团整体上市路径愈发清晰2020-02-18
-
智慧医院2.0时代,详解智慧医院建设路径与领域组成2020-02-08
-
李彦宏发全员信:百度AI成为疫情突破重点算法2020-02-03
-
对话HERE亚太区高级副总裁Stanimira Koleva:海外图商曲线入华背后2020-01-22
-
联邦学习开源社区FATE年末升级:首度支持纵向联邦神经网络算法2020-01-17
-
小米手表再更新:新增英超级专业算法,续航大幅提升2020-01-17
-
算法可检测生命体征,远程医疗即将来临?2020-01-15